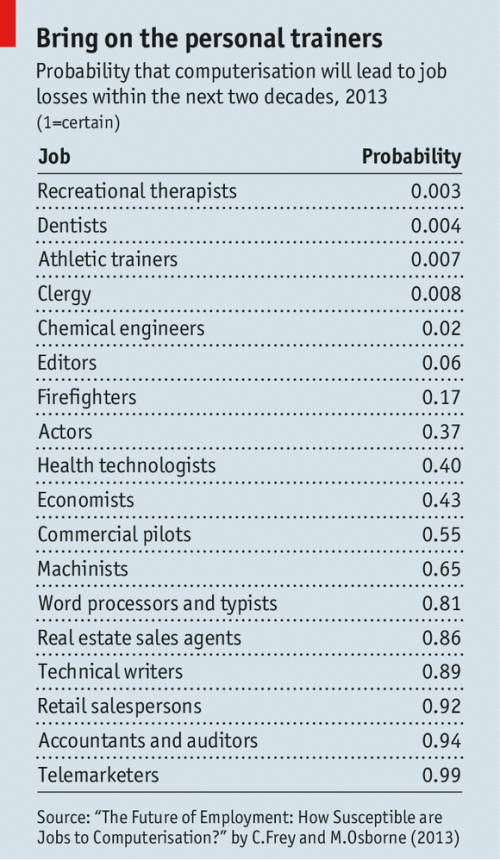
We had some questions on the Stan list regarding identification. The topic arose because people were fitting models with improper posterior distributions, the kind of model where there’s a ridge in the likelihood and the parameters are not otherwise constrained.
I tried to help by writing something on Bayesian identifiability for the Stan list. Then Ben Goodrich came along and cleaned up what I wrote. I think this might be of interest to many of you so I’ll repeat the discussion here.
Here’s what I wrote:
Identification is actually a tricky concept and is not so clearly defined. In the broadest sense, a Bayesian model is identified if the posterior distribution is proper. Then one can do Bayesian inference and that’s that. No need to require a finite variance or even a finite mean, all that’s needed is a finite integral of the probability distribution.
That said, there are some reasons why a stronger definition can be useful:
1. Weak identification. Suppose that, with reasonable data, you’d have a posterior with a sd of 1 (or that order of magnitude). But you have sparse data or collinearity or whatever, and so you have some dimension in your posterior that’s really flat, some “ridge” with a sd of 1000. Then it makes sense to say that this parameter or linear combination of parameters is only weakly identified. Or one can say that it’s identified from the prior but not the likelihood.
If we wanted to make this concept of “weak identification” more formal, we could stipulate that the model is expressed in terms of some hyperparameter A which is set to a large value, and that weak identifiability corresponds to nonidentifiability when A -> infinity.
Even there, though, some tricky cases arise. For example, suppose your model includes a parameter p that is defined on [0,1] and is given a Beta(2,2) prior, and suppose the data don’t tell us anything about p, so that our posterior is also Beta(2,2). That sounds nonidentified to me, but it does have a finite integral.
2. Aliasing. Consider an item response model or
ideal point model or mixture model where the direction or labeling is unspecified. Then you can have 2 or 4 or K! different reflections of the posterior. Even if all priors are proper, so the full posterior is proper, it contains all these copies so this labeling is not identified in any real sense.
Here, and in general, identification depends not just on the model but also on the data. So, strictly speaking, one should not talk about an “identifiable model” but rather an ‘identifiable fitted model” or “identifiable parameters” within a fitted model.
Ben supplied some more perspective. First, in reaction to my definition that a Bayesian model is identified if the posterior distribution is proper, Ben said he agreed, but in that case “what good is the word ‘identified’? If the posterior distribution is improper, then there is no Bayesian inference.”
I agree with Ben, indeed the concept of identification is less important in the Bayesian world than elsewhere. For a Bayesian, it’s generally not a black-and-white issue (“identified” or “not identified”) but rather shades of gray: considering some parameter or quantity of inference (qoi), how much information is supplied by the data. This suggests some sort of continuous measure of identification: for any qoi, corresponding to how far the posterior, p(qoi|y), is from the prior, p(qoi).
Ben continues:
I agree that a lot of people use the word identification without defining what they mean, but there are no shortage of definitions out there. However, I’m not sure that identification is that helpful a concept for the practical problems we are trying to solve here when providing recommendations on how users should write .stan files.
I think many if not most people that think about identification rigorously have in mind a concept that is pre-statistical. So, for them it is going to sound weird to associate “identification” with problems that arise with a particular sample or a particular computational approach. In economics, the idea of identification of a parameter goes back at least to the Cowles Commission guys, such as in the first couple of papers
here.
In causal inference, the idea of identification of an average causal effect is a property of a DAG in Pearl’s
stuff.
I’d like to hold fast to the idea that identification, to the extent it means anything, must be defined as a function of model + data, not just of the model. Sure, with a probability model, you can say that asymptotically you’ll get identification, but asymptotically we’re all dead, and in the meantime we have sparseness and separation and all sorts of other issues.
Ben also had some things to say about my casual use of the term “weak identification” to refer to cases where the model is so weak as to provide very little information about a qoi. Here’s Ben:
Here again we are running into the problem of other people associating the phrase “weak identification” with a different thing (usually instrumental variable models where the instruments are weak predictors of the variable they are instrumenting for).
This paper basically is interested in situations where some parameter is not identified iff another parameter is zero. And then they drift the population toward that zero.
Ben thought my above “A -> infinity” definition was kinda OK but he recommended I not use the term “weak identifiability” which has already been taken. Maybe better for us to go with some measure of the information provided in the shift from prior to posterior. I actually had some of this in my Ph.D. thesis . . .
Regarding my example where the data provide no information on the parameter p defined on (0,1), Ben writes:
Do you mean that a particular sample doesn’t tell us anything about p or that data are incapable of telling us anything about p? In addition, I think it is helpful to distinguish between situations where
(a) There is a unique maximum likelihood estimator (perhaps with probability 1)
(b) There is not a unique maximum likelihood estimator but the likelihood is not flat everywhere with respect to a parameter proposal
(c ) The likelihood is flat everywhere with respect to a parameter proposal
What bothers me about some notion of “computational identifiability” is that a Stan user may be in situation 1 but through some combination of weird priors, bad starting values, too few iterations, finite-precision, particular choice of metric, maladaptation, and / or bad luck can’t get one or more chains to converge to the stationary distribution of the parameters. That’s a practical problem that Stan users face, but I don’t think many people would consider it to be an identification problem.
Maybe something that is somewhat unique to Stan is the idea of identified in the constrained parameter space but not identified in the unconstrained parameter space like we have with uniform sampling on the unit sphere.
Regarding Ben’s remarks above, I don’t really care if there’s a unique maximum likelihood estimator or anything like that. I mean, sure, point estimates do come up in some settings of approximate inference, but I wouldn’t want them to be central to any of our definitions.
Regarding the question of whether identification is defined conditional on the data as well as the model, Ben writes:
Certainly, whether you have computational problems depends on the data, among other things. But to say that identification depends on the data goes against the conventional usage where identification is pre-statistical so we need to think about whether it would be more effective to try to redefine identification or to use other phrases to describe the problems we are trying to overcome.
Hmm, maybe so. Again, this might motivate the quantitative measure of information. For Bayesians, “information” sounds better than “identification” anyway.
Finally, recall that the discussion all started because people were having problems running Stan with improper posteriors or with models with nearly flat priors and where certain parameters were not identified by the data alone. Here’s Ben’s summary of the situation, to best help users:
We should start with the practical Stan advice and avoid the word identifiability. The basic question we are trying to address is “What are the situations where the posterior is proper, but Stan nevertheless has trouble sampling from that posterior?” There is not much to say about improper posteriors, except that you basically can’t do Bayesian inference. Although Stan can optimize a log-likelihood function, everybody doing so should know that you can’t do maximum likelihood inference without a unique maximum. Then, there are a few things that are problematic such as long ridges, multiple modes (even if they are not exactly the same height), label switches and reflections, densities that approach infinity at some point(s), densities that are not differentiable, discontinuities, integerizing a continuous variable, good in the constrained space vs. bad in the constrained space, etc. And then we can suggest what to do about each of these specific things without trying to squeeze them under the umbrella of identifiability.
And that seems like as good as any place to end it. Now I hope someone can get the economists to chill out about identifiability as well. . .
via:http://andrewgelman.com/2014/02/12/think-identifiability-bayesian-inference/
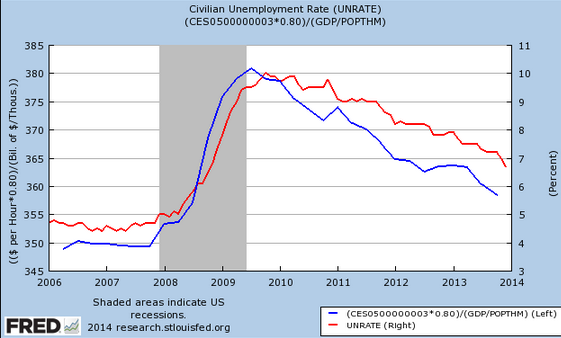 The fit seems better than ever. To my eyes it looks like “real wages” [(nominal average hourly earnings)/(NGDP/pop)] lead unemployment by about a month or two. That’s partly an artifact of a flaw in the St. Louis Fred graphing program. The (W/(GDP/pop)) data for Q4 is put in the October 2013 slot, whereas it should be November 2013. If you shifted the wage series one month to the right the correlation would look even closer.
The fit seems better than ever. To my eyes it looks like “real wages” [(nominal average hourly earnings)/(NGDP/pop)] lead unemployment by about a month or two. That’s partly an artifact of a flaw in the St. Louis Fred graphing program. The (W/(GDP/pop)) data for Q4 is put in the October 2013 slot, whereas it should be November 2013. If you shifted the wage series one month to the right the correlation would look even closer.